Hi,
I am posting here a translated version of the work that Luca Buzzi made and published here: https://www.astrogeo.va.it/astronomia/parallasse15006.php
Credits to him for this very interesting work 😀

Parallax is the difference in the apparent position of an object viewed along two different lines of sight. We can notice it in everyday’s life, when we alternately open and close our eyes: nearby objects seem to move respect to a distant background.
Knowing the angular displacement and the baseline, we can calculate the distance of the object, even astronomical objects. In this case, the baseline must be the greatest possible.
To measure the distance of the Moon, for example, we have to observe it at the same time from two locations separated by hundreds of km. For the parallax of nearby planets or asteroids, the baseline must be thousands of km. For stars, it must be hundreds of millions of km: usually the diameter of the Earth’s orbit.
To measure the parallax of an astronomical object is a very good educational activity, involving photography, astrometry and spherical trigonometry.
In the past days I’ve tried to compute the parallax of the main-belt asteroid (15006) Samcristoforetti, discovered by my good friend Maura Tombelli from Asiago Observatory in 1998, and dedicated to the first Italian female astronaut Samantha Cristoforetti.
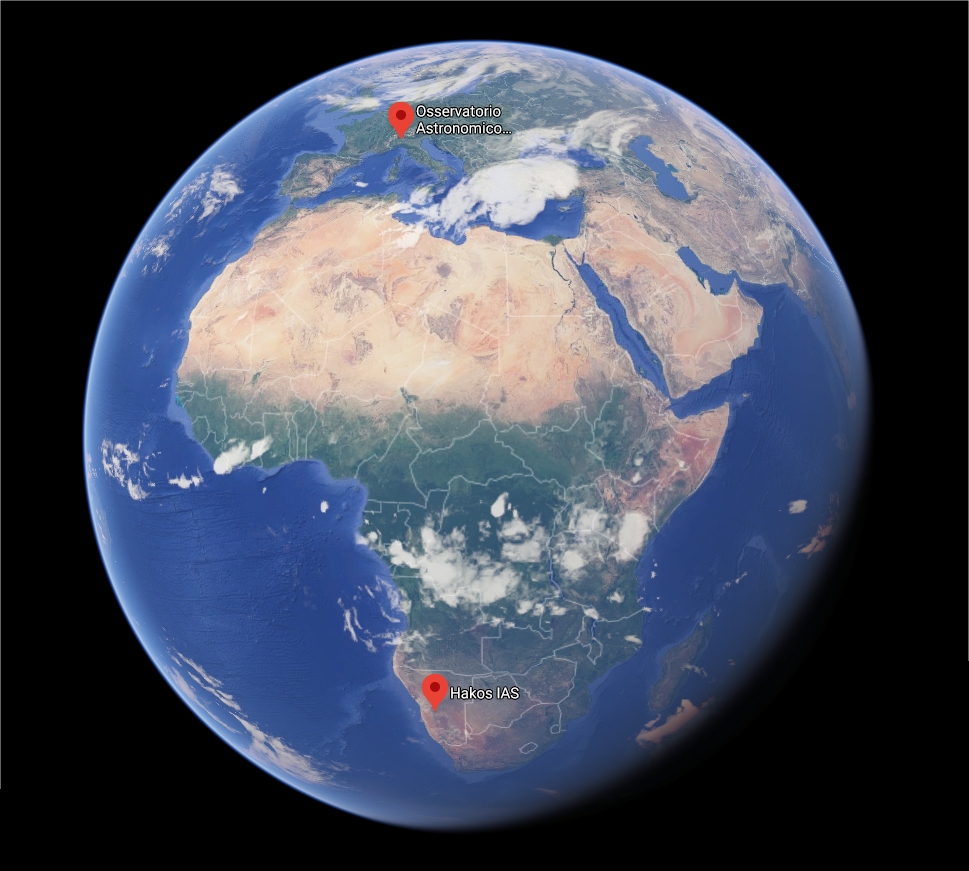
To do this, I needed another telescope in addition to the 0.84-m of the Schiaparelli Astronomical Observatory in Italy, where I work. Since the beginning of March I’m using the 20" AG iDK telescope from Skygems Remote Observatory in Namibia to do some scientific activities regarding southern Near-Earth asteroids and comets.
Namibia skies are one of the most pristine, less light polluted in the world, with many clear nights per year and good seeing.

The night between 2021, Apr. 2nd and 3rd the skies were clear from both sites, so I planned the exposures basically at the same time but with different exposure times, in order to be able to play with the stacks of the images to be sure to have the same average time.
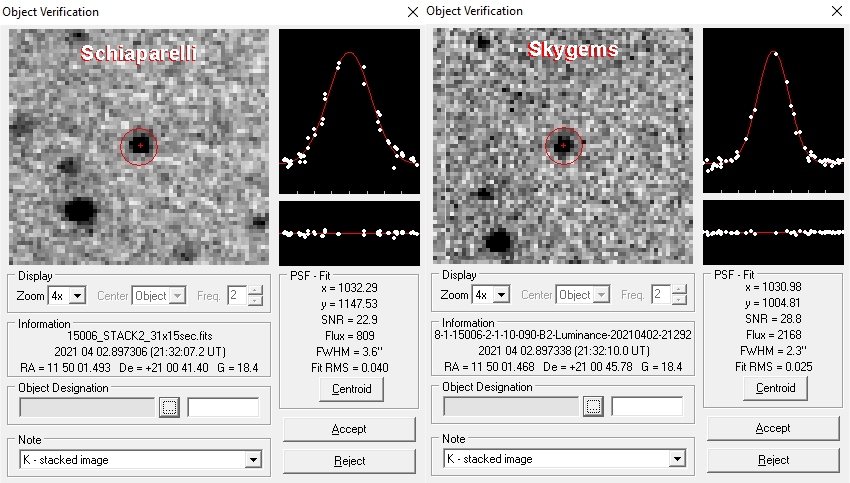
Using Astrometrica I performed the astrometry on both sets of images, and the resulted parallax was 4.34” +/- 0.1”.
Knowing lat/long of both sites I used the following formula:
cos (d) = sen (lat1) * sen (lat2) + cos (lat1) * cos (lat2) * cos (dlong) where dlong is the difference in longitude
to calculate the angular distance between the two sites: 69,44845°.
Then, using:
D = 2 * r * sin (d/2) where r is the Earth radius (6371 km)
I can calculate the baseline: 7258 km.
At last, the asteroid distance is found using
ASTD = D / tang (p) where p is the parallax in degrees
Result was 344.9 million km, in the face of the real distance of 329.4 million km (from NASA Horizons). Difference is less than 5%, and it falls inside the error bar of amateur astrometric measurements (0,3”-0,5”). In fact, the correct parallax should have been 4.55".